버블정렬(Bubble Sort) 알고리즘

저번 포스팅에서는 선택정렬에 대해 공부해보았고 이번에는 버블 정렬에 대해 알아보겠다. 마찬가지로 일련의 숫자들을 오름차순으로 정렬하는 문제이다.

버블 정렬

거품 정렬(Bubble sort)은 두 인접한 원소를 검사하여 정렬하는 방법이다. 시간 복잡도가 O(n^2)로 상당히 느리지만, 코드가 단순하기 때문에 자주 사용된다. 원소의 이동이 거품이 수면으로 올라오는 듯한 모습을 보이기 때문에 지어진 이름이다.

출처 - 위키백과

버블 정렬 또한 선택 정렬과 같이 아주 직관적인 해결방법인데 바로 가까이에 있는 두 숫자끼리 비교를 하여 더 작은 숫자를 앞으로 보내주는 것을 반복하는 것이다.

C++

#include<iostream>

using namespace std;

int main()
{
	int i, j, temp;
	int array[10] = { 1, 10, 5, 8, 7, 6, 4, 3, 2, 9 };

	for (i = 0; i < 10; i++)
	{
		for (j = 0; j < 9 - i; j++) // 버블정렬은 뒤쪽부터 정렬이 되므로 9-i만큼만 반복하면 된다.
		{
			if (array[j] > array[j + 1])
			{
				temp = array[j];
				array[j] = array[j + 1];
				array[j + 1] = temp;
			}
		}
		for (j = 0; j < 10; j++)
		{
			cout << array[j] << " ";
		}
		cout << "\n";
	}

	cout << "결과 :";
	for (i = 0; i < 10; i++)
	{
		cout << array[i] << " ";
	}

	return 0;
}

JavaScript

const bubbleSort = (arr, compare = (prev, next) => prev - next) => {
  const swap = (arr, curIdx, nextIdx) => {
    const curVal = arr[curIdx];
    arr[curIdx] = arr[nextIdx];
    arr[nextIdx] = curVal;
  };

  const len = arr.length;

  for (let i = 0; i < len; i++)
    for (let j = 0; j < len - i - 1; j++)
      if (compare(arr[j], arr[j + 1]) > 0) swap(arr, j, j + 1);
};

(() => {
  const testCase = [
    { arr: [5, 4, 2, 6, 1, 9, 3] },
    { arr: [11, 10, 34, 5, 4, 2, 6, 1, 9, 3] },
    {
      arr: [11, 10, 34, 5, 4, 2, 6, 1, 9, 3],
      compare: (prev, next) => next - prev,
    },
    {
      arr: [[5, 6, 7, 1, 2, 3], [], [1, 2, 3], [4, 2], [6, 4, 7, 3, 1]],
      compare: (prev, next) => prev.length - next.length,
    },
  ];
  testCase.forEach(({ arr, compare }) => {
    bubbleSort(arr, compare);
    console.log(arr);
  });
})();

위와 같이 코드로 표현할 수 있고 아래와 같이 정렬이 진행되는 과정을 확인할 수 있다. 버블 정렬은 뒤쪽부터 정렬이 수행되는 것을 확인할 수 있다.

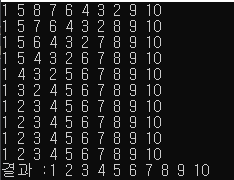
이제 시간복잡도를 확인해 보자. 버블 정렬도 선택 정렬과 마찬가지로 10 + 9 + 8 + 7 + 6 + 5 + .. + 1 만큼 연산을 수행하므로 O(N^2)으로 동일하지만 버블 정렬은 각 싸이클마다 모두 자리를 바꿔주는 연산을 수행하기 때문에 선택 정렬보다 훨씬 비효율적이고 정렬 알고리즘 중에 가장 느린 알고리즘이다.

참조
https://blog.naver.com/ndb796/221226803544 > https://ko.wikipedia.org/wiki/%EA%B1%B0%ED%92%88_%EC%A0%95%EB%A0%AC

Algorithm

버블 정렬

FEATURED TAGS

FRIENDS