선택정렬(Selection Sort) 알고리즘

이제 종강도 했으니 알고리즘 공부를 다시 시작해보려 한다. 유튜버 나동빈님의 강의를 보면서 하나씩 천천히 정리해 나가도록 해보자. 일반적으로 알고리즘을 공부할 때 가장 먼저 풀어보는 문제는 정렬 문제인데, 왜냐면 정렬만큼 알고리즘의 효율성 차이를 극명하게 보여주기 때문이라고 한다. 그래서 여러가지의 정렬 알고리즘을 먼저 배우고 알고리즘의 시간 복잡도에 대해 단계적으로 이해해 보자.

선택 정렬(Selection Sort)

선택 정렬
선택 정렬은 제자리 정렬 알고리즘의 하나로, 다음와 같은 순서로 이루어진다.

주어진 리스트 중에 최소값을 찾는다

그 값을 맨 앞에 위치한 값과 교체한다.(패스)

맨 처음 위치를 뺀 나머지 리스트를 같은 방법으로 교체한다.

출처 - 위키백과

위의 설명처럼 선택 정렬은 가장 작은 것을 선택해서 제일 앞으로 보내는 알고리즘이다. 예를 들어, 3 1 2 5 4 라는 순서의 숫자들을 오름차순으로 정렬한다고 생각해보자. 먼저 리스트의 최솟값을 구하여 가장 앞의 숫자와 위치를 바꾸게 되면 1이 최솟값이므로 3과 자리를 바꾸어 1 3 2 5 4 가 된다. 다음 1을 뺀 나머지의 리스트의 최솟값은 2 이므로 3과 자리를 바꾸어 1 2 3 5 4가 되고, 다음은 3이 최솟값이므로 넘어가서 같은 과정을 반복하면 1 2 3 4 5 로 오름차순 정렬이 끝나게 된다.

C++

#include<iostream>

using namespace std;

int main()
{
	int i, j, min, index, temp; // min : 최솟값, index : 최솟값의 인덱스
	int array[10] = { 1, 10, 5, 8, 7, 6, 4, 3, 2, 9 };

	for (i = 0; i < 10; i++)
	{
		min = 9999;
		for (j = i; j < 10; j++)
		{
			if (array[j] < min) // 최솟값을 구함
			{
				min = array[j];
				index = j;
			}
		}
		temp = array[i]; // 최솟값과 자리 바꾸기
		array[i] = min;
		array[index] = temp;


		for (j = 0; j < 10; j++)
		{
			cout << array[j] << " ";
		}
		cout << "\n";
	}


	cout << "결과 :";
	for (i = 0; i < 10; i++)
	{
		cout << array[i] << " ";
	}

	return 0;

}

JavaScript

const selectionSort = arr => {
  const swap = (arr, curIdx, targetIdx) => {
    const curVal = arr[curIdx];
    arr[curIdx] = arr[targetIdx];
    arr[targetIdx] = curVal;
  };

  const len = arr.length;
  let minIdx;

  for (let i = 0; i < len; i++) {
    minIdx = i;

    for (let j = i; j < len; j++) {
      minIdx = arr[minIdx] > arr[j] ? j : minIdx;
    }

    swap(arr, i, minIdx);
  }
};

(() => {
  const testCase = [
    [5, 4, 2, 6, 1, 9, 3],
    [11, 10, 34, 5, 4, 2, 6, 1, 9, 3],
  ];
  testCase.forEach(arr => {
    selectionSort(arr);
    console.log(arr);
  });
})();

위와 같이 선택정렬을 작성할 수 있다. 또한 아래와 같이 정렬이 진행되는 과정을 확인할 수 있다. 선택 정렬은 앞쪽부터 정렬이 수행되는 것을 확인할 수 있다.

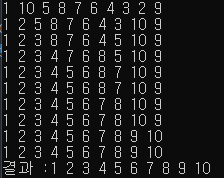
이제 선택 정렬을 수행하는데에 얼마만큼의 시간이 걸리는지를 시간복잡도로 표현할 수 있는데 계산 방법은 다음과 같다.

1 2 3 4 5 6 7 8 9 10 의 10개의 수를 정렬한다고 생각하면

10 + 9 + 8 + … + 1 의 수 만큼 비교연산을 수행해야 한다. 즉, 10 * (10 + 1) / 2 = 55

즉, N개의 수가 있을 때 연산의 횟수는 N * (N + 1) / 2 이다. 따라서 시간복잡도는 O(n^2)이다.

참조
https://blog.naver.com/ndb796/221226800661 > https://ko.wikipedia.org/wiki/%EC%84%A0%ED%83%9D_%EC%A0%95%EB%A0%AC

Algorithm

선택 정렬(Selection Sort)

선택 정렬

FEATURED TAGS

FRIENDS