이번에는 삽입 정렬에 대해 알아보겠다. 앞서 다루었던 정렬 알고리즘과 같은 시간복잡도인 O(N^2)을 가진다.
삽입 정렬(Selection Sort)
삽입 정렬(揷入整列, insertion sort)은 자료 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여, 자신의 위치를 찾아 삽입함으로써 정렬을 완성하는 알고리즘이다.
출처 - 위키백과
삽입 정렬은 각 숫자를 적절한 위치에 삽입하는 방법으로 문제를 해결한다. 다른 정렬 방식들은 무조건 위치를 바꾸는 방식이었다면 삽입 정렬은 필요할 때만 위치를 바꾸게 된다. 이와 같은 특성 때문에 선택 정렬이나 버블 정렬보다 빠르며 어느정도 정렬이 되어있는 경우에서는 아주 빠르게 동작하기도 한다.
삽입 정렬은 현재 위치의 숫자가 앞의 숫자들의 어느 위치에 들어갈지 찾아 적절한 위치에 삽입되는 방식이다.
동작
삽입 정렬은 두 번째 원소부터 시작하여 그 앞(왼쪽)의 원소들과 비교하여 삽입할 위치를 지정한 후 원소를 뒤로 옮기고 지정한 자리에 원소를 삽입하여 정렬하는 알고리즘이다.
즉, 두 번째 원소는 첫 번째 원소, 세 번째 원소는 두 번째와 첫 번째 원소, 네 번째 원소는 세 번째, 두 번째, 첫 번째 원소와 비교한 후 원소가 삽입될 위치를 찾는다. 원소가 삽입될 위치를 찾았다면 그 위치에 원소를 삽입하기 위해 원소를 한 칸씩 뒤로 이동시킨다.
처음 Key 값은 두 번째 원소부터 시작한다.
C++
1 |
|
JavaScript
1 |
|
삽입 정렬은 위와 같이 구현할 수 있으며 진행 과정은 아래와 같다.
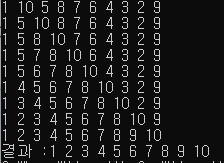
중간 과정에도 앞부분은 계속해서 정렬이 되어있는 것을 확인할 수 있다. 삽입 정렬은 앞서 말했듯이 선택 정렬과 버블 정렬보다는 뛰어나지만 최악의 경우는 앞의 정렬 방식과 같은 수만큼 연산이 일어난다. (O(N^2)) 하지만 2 3 4 5 6 7 8 9 10 1 과 같이 거의 정렬이 된 상태의 경우에는 아주 빠른 속도로 정렬이 가능하다.
참조
https://blog.naver.com/ndb796/221226806398
https://ko.wikipedia.org/wiki/%EC%82%BD%EC%9E%85_%EC%A0%95%EB%A0%AC
https://gmlwjd9405.github.io/2018/05/06/algorithm-insertion-sort.html