퀵 정렬(Quick Sort) 알고리즘

이전까지 봤던 정렬 알고리즘은 모두 시간복잡도 O(N^2)를 가지는 알고리즘이었다. 이러한 시간복잡도를 가지는 알고리즘은 사실상 데이터의 갯수가 커지면 일반적인 상황에서 사용하기가 매우 어렵다. 그렇기 때문에 더욱 빠른 알고리즘이 필요한데 그 대표적인 빠른 알고리즘이 퀵 정렬 알고리즘이다.

퀵 정렬(Quick Sort)

퀵 정렬은 분할 정복(divide and conquer) 방법을 통해 리스트를 정렬한다.

리스트 가운데서 하나의 원소를 고른다. 이렇게 고른 원소를 피벗이라고 한다.

피벗 앞에는 피벗보다 값이 작은 모든 원소들이 오고, 피벗 뒤에는 피벗보다 값이 큰 모든 원소들이 오도록 피벗을 기준으로 리스트를 둘로 나눈다. 이렇게 리스트를 둘로 나누는 것을 분할이라고 한다. 분할을 마친 뒤에 피벗은 더 이상 움직이지 않는다.

분할된 두 개의 작은 리스트에 대해 재귀(Recursion)적으로 이 과정을 반복한다. 재귀는 리스트의 크기가 0이나 1이 될 때까지 반복된다.

재귀 호출이 한번 진행될 때마다 최소한 하나의 원소는 최종적으로 위치가 정해지므로, 이 알고리즘은 반드시 끝난다는 것을 보장할 수 있다.

출처 - 위키백과

퀵 정렬은 대표적인 ‘분할 정복’ 알고리즘으로 평균 속도가 O(N*logN)이다. 이때 logN`은 사실상 거의 상수라고 해도 무방할 만큼 작은 수이다.

예를 들어, 2^10 이 약 1,000 이고 2^20이 약 1,000,000 이므로 N이 1,000,000이라 하더라도

$log_2N = 20$

밖에 되지 않는다. 즉, 굉장히 빠르다는 것을 알 수 있다.

퀵 정렬은 하나의 큰 문제를 두 개의 작은 문제로 분할하는 식으로 빠르게 정렬한다. 더 쉽게 말하자면 특정한 값을 기준으로 큰 숫자와 작은 숫자를 서로 교환한 뒤에 배열을 반으로 나눈다.

일반적으로 퀵 정렬 같은 경우는 피벗 값을 설정할 때 가장 앞에 있는 수를 피벗 값으로 설정한다.

3 7 8 1 5 9 6 10 2 4 에서 시작한다고 하면 피벗 값은 3이다.

이후 왼쪽에서 오른쪽으로 이동하며 피벗 값보다 큰 값 을 찾고 오른쪽부터 왼쪽으로 이동하며 피벗 값보다 작은 값 을 찾는다. 찾으면 두 값의 위치를 바꾸어준다.

3 2 8 1 5 9 6 10 7 4

피벗 값은 3으로 유지하고 같은 방식으로 왼쪽에서 큰 값(8)과 오른쪽에서 작은 값(1)을 구해 바꿔주면

3 2 1 8 5 9 6 10 7 4

이 되며 한 번 더 수행하면 마찬가지로 8과 1 인데 엇갈린 상태가 된다. 즉, 작은 값의 인덱스가 큰 값의 인덱스보다 작아지게 되면 엇갈린 상태인 것이다. 이때는 왼쪽에 있는 값(더 작은값)과 피벗 값인 3과 바꿔주면 된다.

1 2 3 8 5 9 6 10 7 4

여기까지 된다면 3은 정렬이 된 것이고 한 번 분할이 완료된 것이다. 3보다 왼쪽에 있는 수들은 모두 3보다 작고, 3보다 오른쪽에 있는 수들은 모두 3보다 큰 특징을 가진다.

이제 왼쪽 집합과 오른쪽 집합으로 나누어 피벗 값을 각각 설정하고 다시 퀵 정렬을 수행하게 된다. 왼쪽 집합에서는 1이 피벗 값이고 오른쪽 집합에서는 8이 피벗 값이 된다. 먼저 왼쪽부터 보면 1보다 큰 값은 오른쪽에 있고 작은 값은 없지만 왼쪽에 있다고 가정하고 1이 정렬이 된다.

1 2 3 8 5 9 6 10 7 4

마찬가지로 2도 정렬이 되며 오른쪽 부분을 보면 왼쪽에서부터 8보다 큰 값인 9를 찾고 오른쪽에서부터 8보다 작은 4를 찾게된다. 지금은 엇갈리지 않았으므로 9와 4를 바꿔준다.

1 2 3 8 5 4 6 10 7 9

마찬가지로 10과 7을 선택하게 되고 바꿔준다.

1 2 3 8 5 4 6 7 10 9

여기서 한번 더 수행하면 7과 10이 엇갈린 상태이므로 7과 8의 위치가 바뀌어

1 2 3 7 5 4 6 8 10 9

위와 같이 다시 8을 기준으로 왼쪽 집합과 오른쪽 집합으로 나뉘어 왼쪽은 8보다 작은 값들만, 오른쪽은 8보다 큰 값들만 모이게 된다.

이러한 과정을 계속해서 반복하면 모두 정렬이 수행된다.

퀵 정렬처럼 분할을 하여 연산을 하면 빠른 이유에 대해 조금 더 살펴보면

1 2 3 4 5 6 7 8 9 10 이 있을 때

N^2 = 10 * 10 = 100 인 반면

1 2 3 4 5 -> 5 * 5 = 25

6 7 8 9 10 -> 5 * 5 = 25

가 되므로 분할하여 구한 후 더하면 50이 되며 100보다 훨씬 작은 횟수의 연산으로 정렬을 수행할 수 있다.

이때 2씩 계속해서 나누어지는 과정을 log_(2) N 으로 표현하게 된다.

즉, 데이터의 개수가 N이고 반씩 쪼개 들어가기 때문에 O(N*log_(2) N)이라고 할 수 있다.

C++

#include<iostream>

using namespace std;

int const number = 10;

void quickSort(int* data, int start, int end) // start, end -> 부분집합의 시작과 끝 인덱스
{
	if (start >= end) return; // 원소가 1개인 경우

	int key = start; // 피벗 값 첫번째 원소의 인덱스
	int i = start + 1;
	int j = end;
	int temp;

	while (i <= j) // 엇갈릴 때까지 반복
	{
		while (data[i] <= data[key]) // 키 값보다 큰 값을 만날 때까지 이동
		{
			i++;
		}
		while (data[j] >= data[key] && j > start) // 키 값보다 작은 값을 만날 때까지 이동
		{ // 범위를 넘어가지 않도록 j > start를 걸어줌
			j--;
		}
		if (i > j) // 현재 엇갈린 상태면 작은 값(j)을 키 값과 교체
		{
			temp = data[j];
			data[j] = data[key];
			data[key] = temp;
		}
		else // 엇갈리지 않은 상태라면 i와 j를 교체
		{
			temp = data[j];
			data[j] = data[i];
			data[i] = temp;
		}
	}

	for (int i = 0; i < number; i++)
		cout << data[i] << " ";
	cout << endl;

	quickSort(data, start, j - 1);
	quickSort(data, j + 1, end);
}

int main()
{
	int data[number] = { 1, 10, 5, 8, 7, 6, 4, 3, 2, 9 };

	quickSort(data, 0, number - 1);
	cout << "결과 : ";
	for (int i = 0; i < number; i++)
		cout << data[i] << " ";
}

JavaScript

아래 코드는 피벗 값을 첫 번째 원소로 설정했기 때문에 우측부터 확인하여 피벗 값보다 작은 원소를 찾는다.
- 작은 원소가 없으면 첫 번째 값까지 올 수 있도록 한다.
작은 원소를 찾았다면 이제 좌측부터 피벗 값보다 큰 원소를 찾는다.
- 이 때, 우측부터 찾았던 end 값보다 커지지 않도록 범위를 지정한다.
피벗 값보다 작은 값과 큰 값을 찾았다면 start, end의 값을 서로 교환한다.
start, end가 같아질 때까지 찾지 못했다면 해당 값과 피벗을 교환한다.
결과적으로 피벗 기준으로 왼쪽에는 피벗보다 작은 수, 오른쪽에는 피벗보다 큰 수가 남는다.

const swap = (arr, curIdx, targetIdx) => {
  const curVal = arr[curIdx];
  arr[curIdx] = arr[targetIdx];
  arr[targetIdx] = curVal;
};

const sortPartition = (arr, left, right) => {
  const pivotIdx = left;
  const pivot = arr[pivotIdx];

  let start = left;
  let end = right;

  while (start < end) {
    while (arr[end] > pivot) end -= 1;
    while (start < end && arr[start] <= pivot) start += 1; // 초기에는 arr[start] === pivot

    swap(arr, start, end);
  }

  swap(arr, pivotIdx, start);

  return start;
};

const quickSort = (arr, left, right) => {
  if (left >= right) return;

  const pivotIdx = sortPartition(arr, left, right);
  quickSort(arr, left, pivotIdx - 1);
  quickSort(arr, pivotIdx + 1, right);
};

(() => {
  const testCase = [
    [5, 4, 2, 6, 1, 9, 3],
    [11, 10, 34, 5, 4, 2, 6, 1, 9, 3],
  ];
  testCase.forEach(arr => {
    quickSort(arr, 0, arr.length - 1);
    console.log(arr);
  });
})();

위와 같이 재귀함수를 이용하여 작성할 수 있고 아래와 같이 정렬이 진행된다.

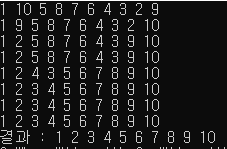
퀵 정렬은 평균 시간 복잡도는 O(N*logN)이지만 최악의 경우 시간 복잡도는 O(N^2)이 되기도 한다. 이미 정렬이 되어있는 경우나 거의 정렬이 되어있는 경우에는 퀵 정렬의 효율이 매우 떨어진다. 반면 삽입 정렬은 이런 경우를 빠르게 해결할 수 있다. 즉, 정렬할 데이터의 특성에 따라 적절한 정렬 알고리즘을 사용하는 것이 중요하다.

참조

https://blog.naver.com/ndb796/221226813382

https://ko.wikipedia.org/wiki/%ED%80%B5_%EC%A0%95%EB%A0%AC

Algorithm

퀵 정렬(Quick Sort)

FEATURED TAGS

FRIENDS