Algorithm

병합 정렬(Merge Sort) 알고리즘

Algorithm

Posted by kwon on 2019-12-27

이번 포스팅에서는 병합 정렬(Merge Sort) 에 대해 알아보겠다. 병합 정렬도 퀵 정렬과 마찬가지로 ‘분할 정복’방법을 채택한 알고르즘이며 결과적으로 퀵 정렬과 동일하게 O(N*logN)의 시간복잡도를 가진다.

퀵 정렬은 피벗 값에 따라서 편향되게 분할할 가능성이 있다는 점에서 최악의 경우 O(N^2)의 시간 복잡도를 가지지만 병합 정렬은 정확히 반절씩 나눈다는 점에서 최악의 경우에도 O(N*logN)을 보장한다.

병합 정렬(Merge Sort)

합병 정렬 또는 병합 정렬(merge sort)은 O(n log n) 비교 기반 정렬 알고리즘이다. 일반적인 방법으로 구현했을 때 이 정렬은 안정 정렬에 속하며, 분할 정복 알고리즘의 하나이다. 존 폰 노이만이 1945년에 개발했다. 하향식 합병 정렬에 대한 자세한 설명과 분석은 1948년 초 헤르만 골드스타인과 폰 노이만의 보고서에 등장하였다.
합병 정렬은 다음과 같이 작동한다.

  1. 리스트의 길이가 1 이하이면 이미 정렬된 것으로 본다. 그렇지 않은 경우에는
  2. 분할(divide) : 정렬되지 않은 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
  3. 정복(conquer) : 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.
  4. 결합(combine) : 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다. 이때 정렬 결과가 임시배열에 저장된다.
  5. 복사(copy) : 임시 배열에 저장된 결과를 원래 배열에 복사한다.

출처 - 위키백과

병합 정렬은 하나의 큰 문제를 두 개의 작은 문제로 분할한 뒤에 각자계산하고 나중에 합치는 방법을 채택한다. 즉, 기본 아이디어는 일단 정확히 반으로 나누고 나중에 정렬하는 것이다.

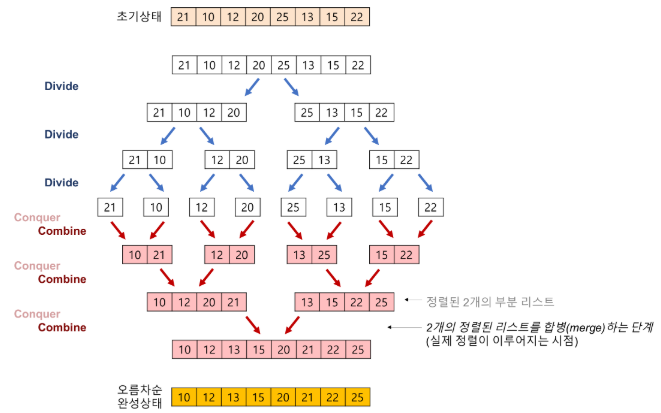
이미지 출처 : https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html

위의 그림처럼 초기 상태의 배열에서 각각 절반씩 계속해서 나누어 크기가 1인 배열로 나눈다. 이후 다시 크기가 1인 배열 두 개씩 병합하며 정렬을 수행한다.(1단계) 그럼 크기가 2인 배열 4개가 되었을 것이고, 4개의 배열은 정렬이 되어있다. 다시 4개의 배열을 두 개씩 병합하여 크기가 4인 배열 2개가 되고, 이 과정에서 정렬이 수행된다.(2단계) 마지막으로 크기가 4인 배열 2개를 병합하여 크기가 8인 배열로 돌아가며 정렬이 된다.(3단계) 이러한 과정으로 진행이 되는데 이때 병합되는 과정은 3단계로 이루어진다. 그 이유는 초기 배열의 크기가 8이기 때문에 log(2)8 = 3 단계가 필요한 것이다.

따라서, 크기가 N인 배열을 정렬한다면 단계는 log(2)N을 유지하게 된다. 또한 데이터의 갯수만큼만 연산하면 되기 때문에 정렬 자체에 필요한 수행시간은 N이다. 결과적으로 총 시간 복잡도는 O(N*logN)이 된다.

위에서 병합이 되는 순간 정렬이 같이 된다고 했다. 그 과정을 한번 살펴보자.

1단계에서는 배열의 크기가 1이기 때문에 두 수만 비교하여 작은 수를 앞에 두면 된다.

2단계에서는 크기가 2인 배열 두 개를 병합하게 되므로 우선 각 배열에서 가장 작은 값을 비교한다. 이때, 각 배열은 정렬되어있는 상태이기 때문에 두 배열의 가장 앞에 있는 값을 서로 비교한다. 위의 그림을 예로 들면 [10, 21]과 [12, 20]에서 먼저 10과 12를 비교하게 되는 것이다. 10이 더 작으므로 10을 새로 만들어질 배열의 맨 앞에 둔다.

그럼 [10, 21]이 있던 배열은 21만 남아있는 상태일 것이다. 그럼 21이 가장 작은 원소이므로 21과 [12, 20]이 들어있는 배열의 최솟값 12와 비교를 하여 12가 더 작으므로 새로 만들어질 배열의 두번째 자리에 12가 들어간다. [10, 12, - , - ] 와 같은 상태일 것이며 이제 남은 [ - , 21] 과 [ - , 20]를 비교하여 더 작은 20이 먼저 들어가 [10, 12, 20, 21]과 같이 정렬이 수행된다.

3단계에서도 2단계와 마찬가지로 두 배열의 최솟값 부터 비교하게 되며 이 과정이 반복되어 정렬이 완료된다.

이러한 과정을 잘 보면 각 부분 집합은 이미 정렬이 된 상태이므로 이미 정렬된 두 배열을 합치는 것은 N번의 연산만 수행하면 된다. 즉 시간 복잡도 O(N)이면 되는 것이다. 즉, 가로축은 N 세로축은 logN이므로 총 시간 복잡도가 O(N*logN)인 것이다.

  • C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
#include<iostream>

using namespace std;

int const number = 8;
int sorted[number]; // 정렬 배열은 반드시 전역 변수로 사용(추가적인 배열)
// 정렬을 수행할 때 추가적인 배열이 필요, 필요할 때마다 배열을 생성한다면 비효율적임
// 전역변수로 모든 함수가 공통적으로 사용하도록 하여 메모리 소모를 최소화

void merge(int a[], int m, int middle, int n) // 두 개의 정렬된 부분 배열을 이용해 새롭게 정렬된 배열을 생성하는 함수
{// m : 시작점 , middle : 중간점, n : 끝점
	int i = m; // 좌측 부분 배열의 시작점
	int j = middle + 1; // 우측 부분 배열의 시작점
	int k = m; // 새로운 배열의 시작점

	// 작은 순서대로 배열에 삽입
	while (i <= middle && j <= n)
	{
		if (a[i] <= a[j])
		{
			sorted[k] = a[i];
			i++;
		}
		else
		{
			sorted[k] = a[j];
			j++;
		}
		k++;
	}
	// 남은 데이터 삽입
	if (i > middle) // 왼쪽 배열이 먼저 모두 삽입된 경우
	{
		for (int t = j; t <= n; t++) // 오른쪽 배열을 순서대로 삽입
		{
			sorted[k] = a[t];
			k++;
		}
	}
	else // 오른쪽 배열이 먼저 모두 삽입된 경우, (j > n)인 경우
	{
		for (int t = i; t <= middle; t++) // 왼쪽 배열을 순서대로 삽입
		{
			sorted[k] = a[t];
			k++;
		}
	}
	// 정렬된 배열을 실제 배열에 삽입
	for (int t = m; t <= n; t++)
		a[t] = sorted[t];

}

void mergeSort(int a[], int m, int n)
{
	int middle;
	// 크기가 1보다 큰 경우
	if (m < n)
	{
		middle = (m + n) / 2;
		mergeSort(a, m, middle);
		mergeSort(a, middle + 1, n);
		merge(a, m, middle, n);
	}
}

void printArray(int a[], int n) // 배열 출력 함수
{
	int i;
	for (i = 0; i < n; i++)
		cout << a[i] << " ";
	cout << endl;
}

int main()
{
	int arr[number] = { 21, 10, 12, 20, 25, 13, 15, 22 };
	printArray(arr, number);
	mergeSort(arr, 0, number - 1);
	printArray(arr, number);
	return 0;
}
  • JavaScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
const mergeSort = (() => {
  const sorted = [];

  const merge = (arr, left, mid, right) => {
    let l = left;
    let m = mid + 1;
    let idx = left;

    while (l <= mid && m <= right) {
      if (arr[l] <= arr[m]) sorted[idx++] = arr[l++];
      else sorted[idx++] = arr[m++];
    }

    while (m <= right) sorted[idx++] = arr[m++]; // 왼쪽이 먼저 삽입된 경우
    while (l <= mid) sorted[idx++] = arr[l++];

    for (let i = left; i <= right; i++) arr[i] = sorted[i];
  };

  return (divideAndMerge = (arr, left, right) => {
    let mid;

    if (left < right) {
      mid = Math.floor((left + right) / 2);

      divideAndMerge(arr, left, mid);
      divideAndMerge(arr, mid + 1, right);
      merge(arr, left, mid, right);
    }
  });
})();

(() => {
  const testCase = [
    [5, 4, 2, 6, 1, 9, 3],
    [11, 10, 34, 5, 4, 2, 6, 1, 9, 3],
    [5, 2, 43, 6, 7, 7, 1, 2],
  ];

  testCase.forEach(arr => {
    mergeSort(arr, 0, arr.length - 1);
    console.log(arr);
  });
})();

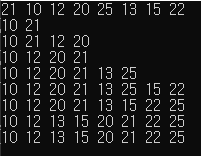
진행 과정을 출력해보면 위와 같은 과정으로 진행이 되는 것을 확인할 수 있다.

병합 정렬을 구현할 때 신경써야 할 부분은 정렬에 사용되는 배열은 전역 변수로 선언해야 한다는 것이다. 만약 함수 안에서 배열을 선언하면 매 번 배열을 선언해야하기 때문에 메모리 낭비가 크다. 이와 같이 병합 정렬은 기존의 데이터를 담을 추가적인 배열 공간이 필요하다는 점에서 메모리 활용이 비효율적인 단점이 있다.

병합 정렬은 일반적인 경우 퀵 정렬보다 느리지만 어떠한 상황에서도 O(N*logN)을 보장한다는 점에서 아주 효율적인 알고리즘이다.

참조
https://blog.naver.com/ndb796/221242106787 > https://ko.wikipedia.org/wiki/%ED%95%A9%EB%B3%91_%EC%A0%95%EB%A0%AC > https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html

FEATURED TAGS
Algorithm
FRIENDS