힙 정렬(Heap Sort) 알고리즘

이번 포스팅에서는 힙 정렬(Heap Sort) 에 대해 알아보겠다. 힙 정렬은 병합 정렬과 퀵 정렬만큼 빠른O(NlogN) 정렬 알고리즘이다. 힙 정렬은 힙 트리 구조(Heap Tree Structure)를 이용하는 정렬 방법이다.

힙 정렬(Heap Sort)

힙 정렬(Heapsort)이란 최대 힙 트리나 최소 힙 트리를 구성해 정렬을 하는 방법으로서, 내림차순 정렬을 위해서는 최대 힙을 구성하고 오름차순 정렬을 위해서는 최소 힙을 구성하면 된다. 최대 힙을 구성하여 정렬하는 방법은 아래 예와 같다.

n개의 노드에 대한 완전 이진 트리를 구성한다. 이때 루트 노드부터 부모노드, 왼쪽 자식노드, 오른쪽 자식노드 순으로 구성한다.

최대 힙을 구성한다. 최대 힙이란 부모노드가 자식노드보다 큰 트리를 말하는데, 단말 노드를 자식노드로 가진 부모노드부터 구성하며 아래부터 루트까지 올라오며 순차적으로 만들어 갈 수 있다.

가장 큰 수(루트에 위치)를 가장 작은 수와 교환한다.

2와 3을 반복한다.
출처 - 위키백과

우선 힙(Heap)이 무엇인지 알아야 한다. 그리고 힙을 알기 전에 이진 트리(Binary Tree)에 대해 알아야 한다. 이진 트리란 컴퓨터 안에서 데이터를 표현할 때 데이터를 각 노드(Node)에 담은 뒤에 노드를 두 개씩 이어 붙이눈 구조이다. 이 때 트리 구조에 맞게 부모 노드에서 자식 노드로 가지가 뻗힌다. 이진 트리는 모든 노드의 자식 노드가 2개 이하인 노드이다.

이진 트리 : 모든 노드의 자식 노드가 2개 이하인 트리 구조

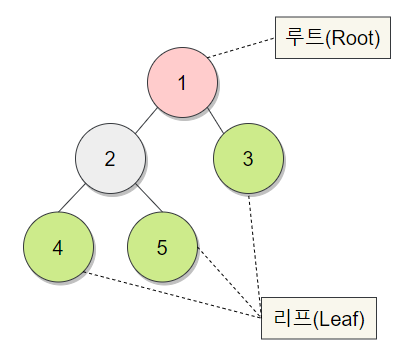
흔히 위와 같은 구조를 이진 트리라고 한다. 이제 완전 이진 트리(Complete Binary Tree) 에 대해 알아보자.

완전 이진 트리는 데이터가 루트(Root)노드부터 시작하여 자식 노드가 왼쪽 자식 노드, 오른쪽 자식 노드로 하나씩 들어가는 구조의 이진 트리이다. 즉, 완전 이진 트리는 이진 트리의 노드가 중간에 비어있지 않고 빽빽히 가득 찬 구조이다.

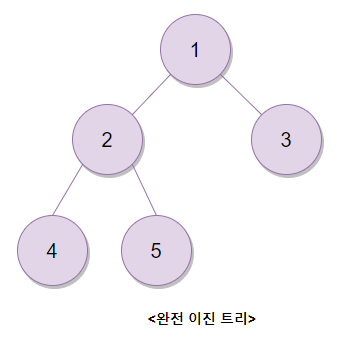
이제 힙(Heap) 에 대해 알아보자. 힙은 최솟값이나 최댓값을 빠르게 찾아내기 위해 완전 이진 트리를 기반으로 하는 트리이다. 힙에는 최대 힙과 최소 힙이 존재하는데 최대 힙은 부모 노드가 자식 노드보다 큰 힙이며 최소 힙은 부모 노드가 자식 노드보다 작은 힙이다.

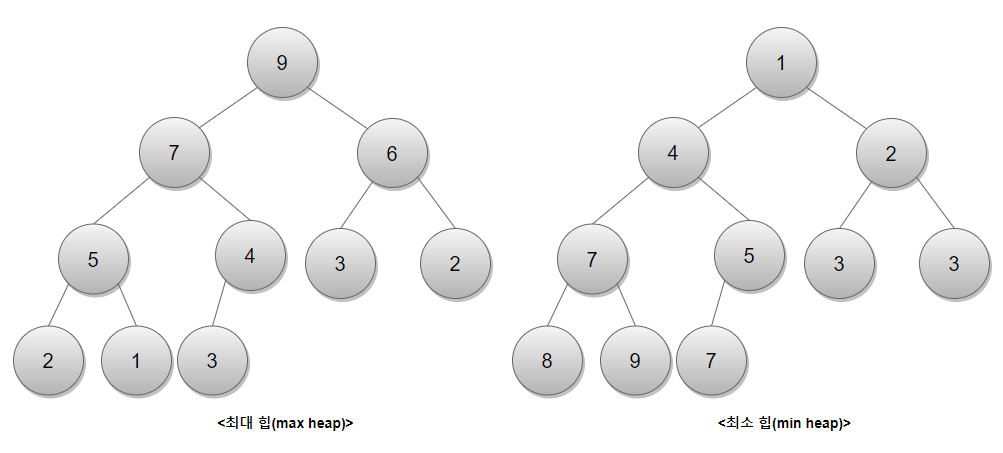
힙은 위와 같은 구조이며 일단 힙 정렬을 하기 위해서는 정해진 데이터를 힙 구조를 가지도록 만들어야 한다.

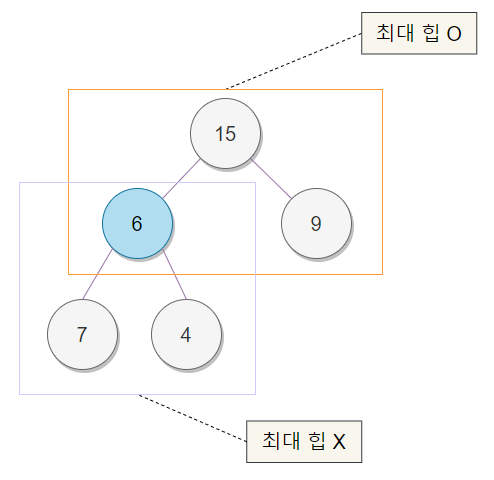
힙 정렬을 수행하기 위해서는 힙 생성 알고리즘(Heapify Algorithm) 을 사용한다. 힙 생성 알고리즘은 특정한 하나의 노드에 대해서 수행하는 것이다. 또한 하나의 노드를 제외하고는 최대 힙이 구성되어 있는 상태를 가정한다는 특징이 있다. 위의 트리에서 6만 최대 힙 정렬을 수행해주면 전체 트리가 최대 힙 구조로 형성되는 상태이다.

힙 생성 알고리즘은 특정한 노드의 두 자식 중에서 더 큰 자식과 자신의 위치를 바꾸는 방식 이다. 또한 위치를 바꾼 뒤에도 여전히 자식이 존재하는 경우 자식이 더이상 존재하지 않을때 까지 자식 중에서 더 큰 자식과 자신의 위치를 바꾸어야 한다. 즉, 위에서 5의 자식인 7과 4 중에서 더 큰 자식인 7과 5의 위치를 바꾸어 주면 된다. 바꾼 결과는 아래와 같다.

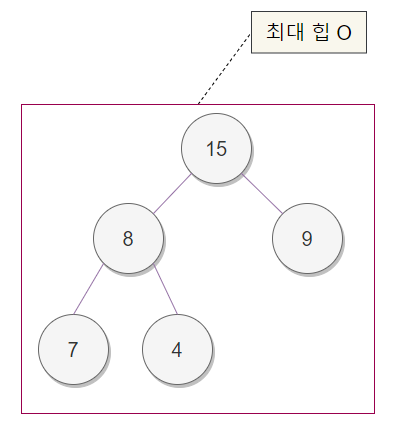
위와 같이 힙 생성 알고리즘은 전체 트리를 힙 구조를 가지도록 만든다는 점에서 굉장히 중요한 알고리즘이다. 이러한 힙 생성 알고리즘의 시간 복잡도는 몇일까? 한 번 자식 노드로 내려갈 때마다 노드의 갯수가 2배씩 증가한다는 점에서 O(logN)이다. 예를 들어 데이터의 갯수가 1024개라면 10번 정도만 내려가도 된다는 뜻이다.

이제 예시를 보며 실제 힙 정렬 과정을 수행해보자.

7 6 5 8 3 5 9 1 6

위의 데이터를 오름차순으로 정렬한다고 해보자. 기본적으로 이진 트리를 표현하는 가장 쉬운 방법은 배열에 그대로 삽입하는 것이다. 현재 정렬할 데이터의 갯수가 9개이기 때문에 인덱스 0붙터 8까지 차례로 담아주면 된다.

0	1	2	3	4	5	6	7	8
7	6	5	8	3	5	9	1	6

다시 말해 완전 이진 트리에 삽입이 되는 순서대로 인덱스를 붙여주는 것이다. 위 배열을 완전 이진 트리 형태로 출력하면 다음과 같다.

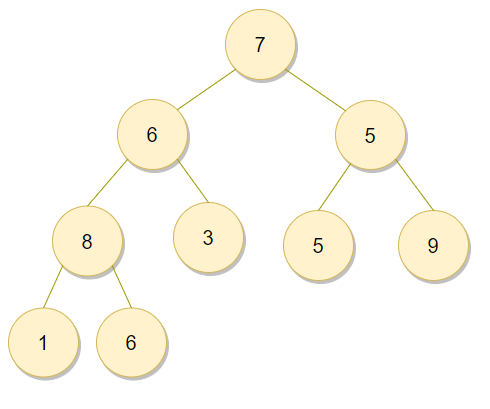
말 그대로 배열에 있는 인덱스가 그대로 차례대로 트리로 표현된 것이다. 위와 같은 상황에서 힙 생성 알고리즘을 적용하여 전체 트리를 힙 구조로 만들면 된다. 이 때 데이터의 갯수가 N개 이므로 전체 트리를 힙 구조로 만드는 복잡도는 O(N*logN)이다.

그래서 결과적으로는 위와 같이 최대 힙이 구성된다. 이제부터 실제로 우리가 원하던 정렬을 직관적으로 수행할 수 있다. 루트(Root)에 있는 값을 가장 뒤쪽으로 보내면서 힙 트리의 크기를 1씩 빼주는 것이다.

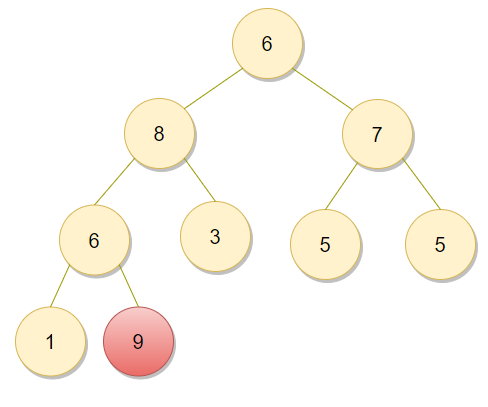
위와 같이 9와 6을 바꾼 뒤에 9는 정렬이 완료된 것이므로 빨간색으로 표현한다. 이제 9를 제외하고 나머지 8개 원소를 기준으로 또 힙 생성 알고리즘(Heapify)를 수행한다. 결과는 다음과 같다.

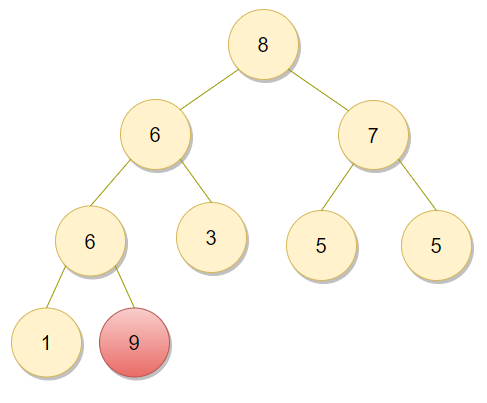
이제 다시 가장 큰 숫자인 8이 루트에 존재한다. 이것을 가장 뒤쪽의 원소와 서로 바꾼다.

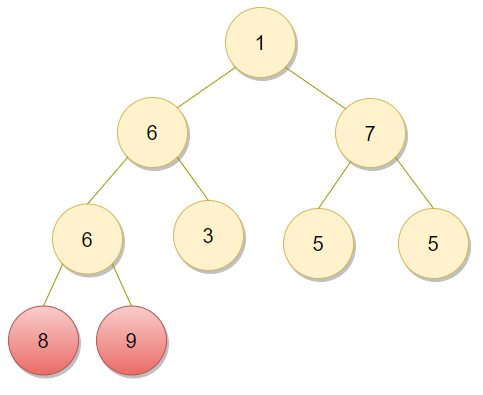
그럼 위와 같이 8과 9가 가장 뒤에 배열되어 정렬된 것을 볼 수 있다. 이제 이 과정을 반복하면 된다. 힙 생성 알고리즘의 시간 복잡도는 O(logN)이고 전체 데이터의 갯수가 N개이므로 결과적으로 힙 정렬의 시간 복잡도는 O(N*logN)이라고 할 수 있다.

#include<iostream>

using namespace std;

int const number = 9;
int heap[number] = { 7, 6, 5, 8, 3, 5, 9, 1, 6 };

void printArray(int a[], int n) // 배열 출력 함수
{
	int i;
	for (i = 0; i < n; i++)
		cout << a[i] << " ";
	cout << endl;
}

int main(void)
{
	int temp;

	printArray(heap, number);
	// 전체 트리 구조를 최대 힙 구조로 바꾼다.
	for (int i = 1; i < number; i++)
	{
		int c = i;
		do
		{
			int root = (c - 1) / 2; // 자기 자신의 부모를 의미
			if (heap[root] < heap[c]) // 부모보다 자식이 크다면 위치를 바꿈
			{
				int temp = heap[root];
				heap[root] = heap[c];
				heap[c] = temp;
			}
			c = root; // 부모의 인덱스로 변환하여 0이 될때까지 올라감
		} while (c != 0);
	}
	printArray(heap, number);

	// 크기를 줄여가며 반복적으로 힙을 구성
	for (int i = number - 1; i >= 0; i--) // 마지막 인덱스부터 시작
	{
		// 가장 큰 값을 맨 뒤로 보냄
		int temp = heap[0];
		heap[0] = heap[i];
		heap[i] = temp;
		int root = 0;
		int c = 1;
		do
		{
			c = 2 * root + 1;
			// 자식 중에 더 큰 값 찾기
			// 옆의 값과 비교하여 더 큰 값의 인덱스를 c에 지정
			if (heap[c] < heap[c + 1] && c < i - 1) // 범위를 넘지 않는 한에서
				c++;
			// 루트보다 자식이 더 크다면 교환
			if (heap[root] < heap[c] && c < i)
			{
				int temp = heap[root];
				heap[root] = heap[c];
				heap[c] = temp;
			}
			root = c; // 자식의 인덱스로 변환하여 정렬되지 않은 마지막 인덱스까지 진행
		} while (c < i); // 정렬된 인덱스 전까지 반복
		printArray(heap, number);
	}
	printArray(heap, number);

}

JavaScript


function* range(start, end) {
  for (let i = start; i <= end; i++) yield i;
}

const swap = (arr, curIdx, targetIdx) => {
  [arr[curIdx], arr[targetIdx]] = [arr[targetIdx], arr[curIdx]];
};

const insertIntoHeap = (heap, value) => {
  heap.push(value);
  let index = heap.length - 1;

  while (index !== 0) {
    const parent = Math.floor(index / 2);
    if (heap[parent] < heap[index]) swap(heap, index, parent);
    index = parent;
  }
};

const deleteMax = heap => {
  const top = heap[0];
  swap(heap, 0, heap.length - 1);
  heap.pop();

  let parent = 0;
  let child = 1;
  const lastIdx = heap.length - 1;

  const next = () => {
    parent = child;
    child = Math.floor(child * 2) + 1;
  };

  while (child <= lastIdx) {
    if (child + 1 <= lastIdx && heap[child] < heap[child + 1]) child += 1;
    if (heap[parent] < heap[child]) swap(heap, parent, child);
    next();
  }

  return top;
};

const heapSort = arr => {
  const heap = [];

  arr.forEach(val => {
    insertIntoHeap(heap, val);
  });

  const heapSize = heap.length;
  const result = [];

  for (const i of range(1, heapSize)) {
    result.push(deleteMax(heap));
  }

  return result;
};

(() => {
  const testCase = [
    [5, 4, 2, 6, 1, 9, 3],
    [11, 10, 34, 5, 4, 2, 6, 1, 9, 3],
    [5, 2, 43, 6, 7, 7, 1, 2],
  ];
  testCase.forEach(arr => {
    console.log(heapSort(arr));
  });
})();

최대 힙을 이용하여 위와 같이 힙 정렬을 작성할 수 있으며 진행 과정은 다음과 같다.

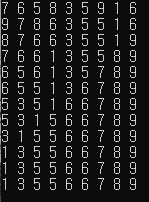
힙 정렬은 병합 정렬과 다르게 별도로 추가적인 배열이 필요하지 않다는 점에서 메모리 측면에서 매우 효율적이다. 또한 항상 O(N*logN)을 보장할 수 있다는 점에서 아주 강력한 알고리즘이다. 하지만 단순히 속도만 놓고 비교하면 퀵 정렬이 평균적으로 더 빠르기 때문에 힙 정렬이 일반적으로 많이 사용되지는 않는다고 한다.

참조
https://blog.naver.com/ndb796/221228342808 > https://ko.wikipedia.org/wiki/%ED%9E%99_%EC%A0%95%EB%A0%AC > https://gmlwjd9405.github.io/2018/05/10/algorithm-heap-sort.html

Algorithm

힙 정렬(Heap Sort)

FEATURED TAGS

FRIENDS