Algorithm

크루스칼(Kruskal Algorithm) 알고리즘

Algorithm

Posted by kwon on 2020-01-09

크루스칼(Kruskal Algorithm)

크루스칼 알고리즘은 가장 적은 비용으로 모든 노드를 연결하기 위해 사용하는 알고리즘이다. 즉, 최소 비용 신장 트리를 만들기 위한 대표적인 알고리즘이라고 할 수 있다. 흔히 여러 개의 도시가 있을 때 각 도시의 도로를 이용해 비용을 최소한으로 연결하고자 할 때 실제로 적용되는 알고리즘이다.

아래의 그래프를 보면 노드는 7개이고 간선의 갯수는 11개이다.

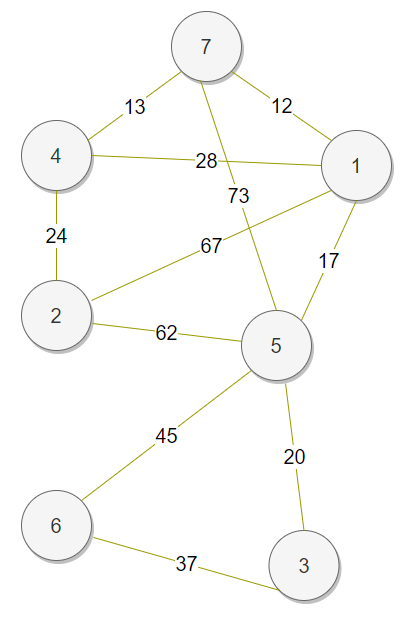
위와 같은 그래프를 최소한의 비용으로 연결만 하고자 한다면 어떻게 해야할까?

일단 모든 노드를 최대한 적은 비용으로 연결만 시키면 되는 것이기 때문에 모든 간선의 정보를 오름차순으로 정렬하여 비용이 적은 간선부터 하나씩 그래프에 포함시키면 될 것이다.

  • 노드 1

    • (1, 7) [12]
    • (1, 4) [28]
    • (1, 2) [67]
    • (1, 5) [17]

  • 노드 2

    • (2, 4) [24]
    • (2, 5) [62]

  • 노드 3

    • (3, 5) [20]
    • (3, 6) [37]

  • 노드 4

    • (4, 7) [13]

  • 노드 3

    • (5, 6) [45]
    • (5, 7) [73]

우선 위와 같이 간선의 정보들을 저장한다. 노드 1부터 노드 7까지 연결된 모든 간선을 정보를 저장한 것이다. 6, 7이 정보가 없는 이유는 이미 다른 노드들의 간선 정보에 모두 포함되었기 때문이다. 이렇게 총 11개의 간선 정보를 간선의 비용을 기준으로 오름차순 정렬을 수행해보자.

  • 정렬된 간선 정보
    • (1, 7) [12]
    • (4, 7) [13]
    • (1, 5) [17]
    • (3, 5) [20]
    • (2, 4) [24]
    • (1, 4) [28]
    • (3, 6) [37]
    • (5, 6) [45]
    • (2, 5) [62]
    • (1, 2) [67]
    • (5, 7) [73]

이제 다음과 같은 규칙에 따라 그래프를 연결하면 된다.

  1. 정렬된 순서에 맞게 그래프에 포함시킨다.
  2. 포함시키기 전에는 사이클 테이블을 확인한다.
  3. 사이클을 형성하는 경우 간선을 포함하지 않는다.

여기서 사이클은 그래프가 서로 연결되어 아래와 같이 사이클을 형성하는 경우이다. 최소 비용 신장 트리에서는 사이클이 발생하면 안된다. 모든 노드를 연결하기만 하면 되는데 사이클이 발생한다는 것은 이미 연결된 노드끼리 다시 연결한다는 뜻이기 때문이다.

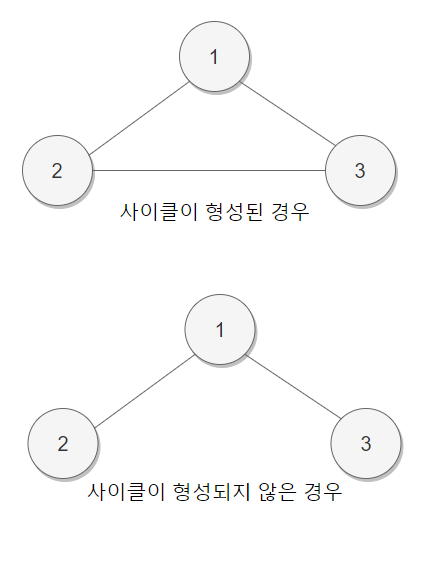
사이클이 발생의 여부는 저번 포스팅의 Union-Find 알고리즘을 적용하여 구할 수 있다.

초기 상태는 다음과 같을 것이다.

  • 정렬된 간선 정보
    • (1, 7) [12]
    • (4, 7) [13]
    • (1, 5) [17]
    • (3, 5) [20]
    • (2, 4) [24]
    • (1, 4) [28]
    • (3, 6) [37]
    • (5, 6) [45]
    • (2, 5) [62]
    • (1, 2) [67]
    • (5, 7) [73]
  • 사이클 테이블
    노드 번호
    1
    2
    3
    4
    5
    6
    7
    부모 노드 번호 1 2 3 4 5 6 7

이제 첫 번째 간선부터 시작하면

첫 번째 간선 선택

  • 정렬된 간선 정보

    • (1, 7) [12]
    • (4, 7) [13]
    • (1, 5) [17]
    • (3, 5) [20]
    • (2, 4) [24]
    • (1, 4) [28]
    • (3, 6) [37]
    • (5, 6) [45]
    • (2, 5) [62]
    • (1, 2) [67]
    • (5, 7) [73]

  • 사이클 테이블

    노드 번호
    1
    2
    3
    4
    5
    6
    7
    부모 노드 번호 1 2 3 4 5 6 1

  • 그래프 상태

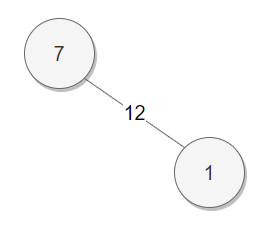
두 번째 간선 선택

  • 정렬된 간선 정보

    • (1, 7) [12]
    • (4, 7) [13]
    • (1, 5) [17]
    • (3, 5) [20]
    • (2, 4) [24]
    • (1, 4) [28]
    • (3, 6) [37]
    • (5, 6) [45]
    • (2, 5) [62]
    • (1, 2) [67]
    • (5, 7) [73]

  • 사이클 테이블

    노드 번호
    1
    2
    3
    4
    5
    6
    7
    부모 노드 번호 1 2 3 1 5 6 1

  • 그래프 상태

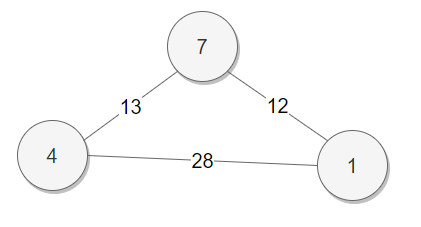
세 번째 간선 선택

  • 정렬된 간선 정보

    • (1, 7) [12]
    • (4, 7) [13]
    • (1, 5) [17]
    • (3, 5) [20]
    • (2, 4) [24]
    • (1, 4) [28]
    • (3, 6) [37]
    • (5, 6) [45]
    • (2, 5) [62]
    • (1, 2) [67]
    • (5, 7) [73]

  • 사이클 테이블

    노드 번호
    1
    2
    3
    4
    5
    6
    7
    부모 노드 번호 1 2 3 1 1 6 1

  • 그래프 상태

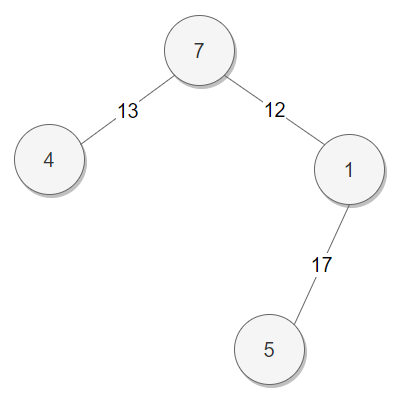
네 번째 간선 선택

  • 정렬된 간선 정보

    • (1, 7) [12]
    • (4, 7) [13]
    • (1, 5) [17]
    • (3, 5) [20]
    • (2, 4) [24]
    • (1, 4) [28]
    • (3, 6) [37]
    • (5, 6) [45]
    • (2, 5) [62]
    • (1, 2) [67]
    • (5, 7) [73]

  • 사이클 테이블

    노드 번호
    1
    2
    3
    4
    5
    6
    7
    부모 노드 번호 1 2 1 1 1 6 1

  • 그래프 상태

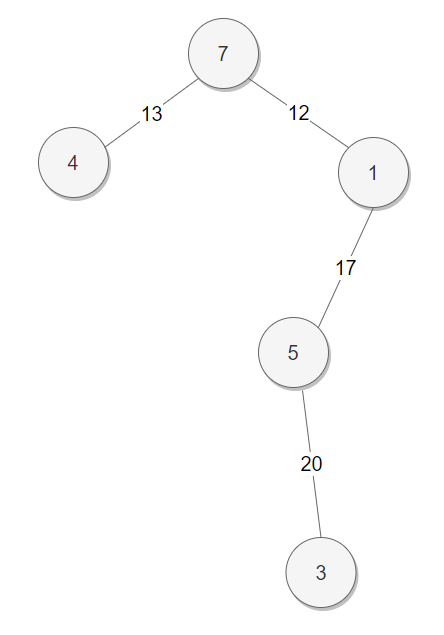
다섯 번째 간선 선택

  • 정렬된 간선 정보

    • (1, 7) [12]
    • (4, 7) [13]
    • (1, 5) [17]
    • (3, 5) [20]
    • (2, 4) [24]
    • (1, 4) [28]
    • (3, 6) [37]
    • (5, 6) [45]
    • (2, 5) [62]
    • (1, 2) [67]
    • (5, 7) [73]

  • 사이클 테이블

    노드 번호
    1
    2
    3
    4
    5
    6
    7
    부모 노드 번호 1 1 1 1 1 6 1

  • 그래프 상태

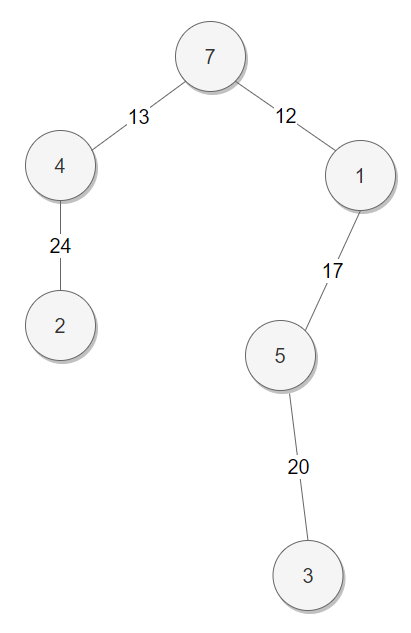
여섯 번째 간선 선택
  • 정렬된 간선 정보
    • (1, 7) [12]
    • (4, 7) [13]
    • (1, 5) [17]
    • (3, 5) [20]
    • (2, 4) [24]
    • (1, 4) [28]
    • (3, 6) [37]
    • (5, 6) [45]
    • (2, 5) [62]
    • (1, 2) [67]
    • (5, 7) [73]

이 때 1과 4가 이미 연결되어 있으므로 무시하고 넘어간다. 사이클 테이블의 값이 서로 동일한 것을 보면 된다.

  • 사이클 테이블

    노드 번호
    1
    2
    3
    4
    5
    6
    7
    부모 노드 번호 1 1 1 1 1 6 1

  • 그래프 상태

일곱 번째 간선 선택

  • 정렬된 간선 정보

    • (1, 7) [12]
    • (4, 7) [13]
    • (1, 5) [17]
    • (3, 5) [20]
    • (2, 4) [24]
    • (1, 4) [28]
    • (3, 6) [37]
    • (5, 6) [45]
    • (2, 5) [62]
    • (1, 2) [67]
    • (5, 7) [73]

  • 사이클 테이블

    노드 번호
    1
    2
    3
    4
    5
    6
    7
    부모 노드 번호 1 1 1 1 1 1 1

  • 그래프 상태

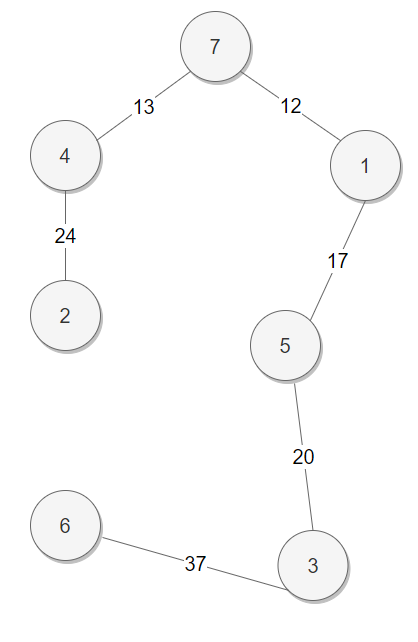
위와 같이 사이클 테이블의 값이 모두 1이 되며 최소 비용 신장 트리가 완성된 것을 볼 수 있다. 나머지 남은 4개의 간선은 모두 연결되어 있으므로 스킵하여 다음과 같이 완성된다.

완성
  • 정렬된 간선 정보
    • (1, 7) [12]
    • (4, 7) [13]
    • (1, 5) [17]
    • (3, 5) [20]
    • (2, 4) [24]
    • (1, 4) [28]
    • (3, 6) [37]
    • (5, 6) [45]
    • (2, 5) [62]
    • (1, 2) [67]
    • (5, 7) [73]

  • 사이클 테이블

    노드 번호
    1
    2
    3
    4
    5
    6
    7
    부모 노드 번호 1 1 1 1 1 1 1

  • 그래프 상태

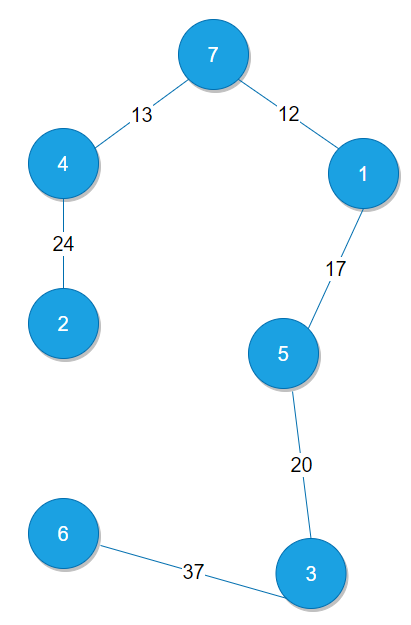
따라서 총 비용은 12 + 13 + 17 + 20 + 24 + 37 = 123 이 된다. 코드로 구현해 보면 다음과 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
#include<iostream>
#include<vector>
#include<algorithm>

using namespace std;

class Edge // 하나의 간선 정보를 담는 클래스
{
public:
	int node[2]; // 서로 연결된 두 개의 노드 정보
	int distance; // 비용 정보
	Edge(int a, int b, int distance)
	{
		this->node[0] = a;
		this->node[1] = b;
		this->distance = distance;
	}
	bool operator < (Edge &edge)
	{
		return this->distance < edge.distance; // 거리가 작은 간선이 먼저 출력
	}
};

// 부모 노드를 찾는 함수
int getParent(int parent[], int x)
{
	if (parent[x] == x)	return x; // 부모 노드가 자신인 경우 리턴
	else return parent[x] = getParent(parent, parent[x]);
	// 부모 노드의 값과 자신이 다르다면 재귀 호출
}

// 두 부모 노드를 합치는 함수
void unionParent(int parent[], int a, int b)
{
	a = getParent(parent, a); // a의 부모 노드 확인
	b = getParent(parent, b); // b의 부모 노드 확인
	if (a < b) parent[b] = a; // 더 작은 값을 부모 노드로 지정
	else parent[a] = b;
}

// 같은 부모를 가지는지 확인
int findParent(int parent[], int a, int b)
{
	a = getParent(parent, a); // a의 부모 노드 확인
	b = getParent(parent, b); // b의 부모 노드 확인
	if (a == b) return 1; // 같은 부모를 가진다면 1을 리턴
	else return 0; // 다르다면 0리턴
}

int main(void)
{
	int const node = 7; // 노드의 개수
	int line = 11; // 간선의 개수

	vector<Edge> v; // 간선 정보를 담을 벡터
	// 11개의 간선 정보를 벡터에 담음
	v.push_back(Edge(1, 7, 12));
	v.push_back(Edge(1, 4, 28));
	v.push_back(Edge(1, 2, 67));
	v.push_back(Edge(1, 5, 17));
	v.push_back(Edge(2, 4, 24));
	v.push_back(Edge(2, 5, 62));
	v.push_back(Edge(3, 5, 20));
	v.push_back(Edge(3, 6, 37));
	v.push_back(Edge(4, 7, 13));
	v.push_back(Edge(5, 6, 45));
	v.push_back(Edge(5, 7, 73));

	// 간선의 비용을 기준으로 오름차순 정렬
	sort(v.begin(), v.end());

	// 각 정점이 포함된 그래프가 어디인지 저장
	int parent[node];
	for (int i = 0; i < node; i++)
		parent[i] = i;

	int sum = 0; // 합계
	for (int i = 0; i < v.size(); i++)
	{ // 사이클이 발생하지 않는 경우 그래프에 포함
		if (!findParent(parent, v[i].node[0] - 1, v[i].node[1] - 1))
		{ // parent[]는 0부터 시작했기 때문에 각 노드 번호에서 1을 빼줘야 일치함
			sum += v[i].distance; // 연결한 노드의 거리를 누적
			unionParent(parent, v[i].node[0] - 1, v[i].node[1] - 1); // 연결되었으므로 부모를 합침
		}
	}

	cout << sum << endl; // 합계 출력
}

참조
https://blog.naver.com/ndb796/221230994142

FEATURED TAGS
Algorithm
FRIENDS